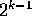It turns out that for some applications pseudo-random numbers are a little too random.
Notice that a scatter plot of pseudo-random numbers has places that are relatively undersampled and other places that have clusters of points.
If we change our generator so as to maintain a nearly uniform density of coverage of the domain then we have a random number generator known as quasi-random number generator.
A scatter plot of some quasi-random numbers, has a distinctly different coverage pattern from pseudo-random numbers. Quasi-random numbers give up serial independence of subsequently generated values in order to obtain as uniform as possible coverage of the domain. This avoids clusters and voids in the pattern of a finite set of selected points.
The generation of these maximally avoiding random numbers requires
a good deal of bit twiddling. We will briefly describe here a rather
efficient method using what is known as a Sobol' sequence.
This method uses a set of binary fractions called direction numbers.
The jth number is generated by doing a bitwise exclusive-or of all
the direction numbers so that the ith bit of the number is nonzero.
The effect is such that the bits toggle on and off at different rates.
The kth bit switches once in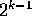 
steps so that the least
significant bit switches the fastest, and the most significant
bit switches the slowest.
A particulary efficient implementation of a quasi-random number generator is uses an idea of Antonov and Saleev (1979), which uses the Gray code of the number instead of the number itself. The use of the Gray code makes the generator very efficient because of the fact that adjacent Gray codes differ from each other in just one bit position. This makes it possible to get the next quasi-random number by just doing one exclusive-or operation.
The direction numbers must be calculated according to the number of dimensions that the quasi-random numbers are to be used in.
The mathematics behind the generation of the direction numbers not trivial, but fortunately not necessary in order to implement and use this generator. For an introduction to the mathematics behind quasi-random numbers, see Press & Teukolsky, 1989.
