The generators mentioned above all generate uniformly distributed values. In order to generate numerical solutions to our SDEs we need Normally or Gaussian distributed random numbers. There are many was of solving this problem (see for example Rubinstein, 1981, for an extensive discussion of this topic) but we will only go into one important method here.
Since we have an equation that describes our desired distribution function, then it may be possible to use a transformation function. This transformation function takes random variables from one distribution as inputs and outputs random variables in a new distribution function. Probably the most important of these transformation functions is known as the Box-Muller (1958) transformation. It allows us to transform uniformly distributed random variables, to a new set of random variables with a Gaussian (or Normal) distribution,
We start with two random numbers,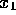 
and 
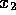, which come from a
uniform distribution (in the range from 0 to 1). Then apply the above
transformation pair to get two new random numbers which have a Gaussian distributionwith zero mean and a standard deviation of 1.
This transformation is somewhat more robust numerically in the polar form,
The polar form takes two uniform floating point numbers (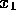 
and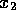 
),
in the range -1 to 1, as inputs it must also be verified that 
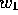in (2) is
less than 1 before using it in (3). The polar transformation also returns two
Gaussian floating point numbers as output ( (4) and (5) ).
The polar form is faster because it does the equivalent
of the sine and cosine geometrically without a call to the trigonometric function
library. It
also is somewhat more robust to numerical problems that can occur when the result
of the base generator returns a value that is
very close to 0.0 or 1.0 (this will eventually happen if
millions of numbers are being generated).