

Next: Quasi-Random Numbers
Up: Random WalksMarkov Chains
Previous: Linear Congruential Generators
Another useful generator uses a shift register sequence. The
implementation known as
R250 (Kirkpatrick and Stoll, 1981)
has several advantages over a linear
congruential generator.
First it has a very long period, 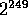 . What is more, this
period does not depend upon the number of bits used in the random
number generator. This makes 16-bit random numbers generated by R250,
adequate for many applications. The very long period makes it suitable for
scientific applications,
such as Monte Carlo and stochastic integration,
where many numbers need to be generated.
. What is more, this
period does not depend upon the number of bits used in the random
number generator. This makes 16-bit random numbers generated by R250,
adequate for many applications. The very long period makes it suitable for
scientific applications,
such as Monte Carlo and stochastic integration,
where many numbers need to be generated.
R250 is also generally much faster to run than an LCG implementation;
this also pays off when many numbers need to be generated.
R250 has an overhead of calling another generator 500 times for set-up,
so if the set-up time is counted there won't be a speed advantage to R250
when only a small number of values are to be generated.
This generator is built from a 1-bit random generator that
is based upon the equation,
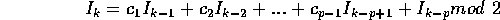
which applies for each bit. The maximum period of this sequence is 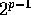 ,
so a large value of p is called for, we will use p = 250.
We now judiciously choose most of the
,
so a large value of p is called for, we will use p = 250.
We now judiciously choose most of the 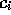 terms to be zero, so that there are
only two terms on the right hand side,
terms to be zero, so that there are
only two terms on the right hand side,

and choose q = 103. This means then, to generate a random bit, we add the
previously calculated 103rd and 250th bits. Now of course, we want to generate
a random number of 16 or 32 bits. Obviously this can be accomplished by doing
the above 1 bit addition for each bit in the desired random number. Noticing
that exclusive-or is the same thing as bitwise addition, then we can do all the
bitwise additions in parallel by using the above equation where the 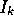 are
now words and the + is exclusive-or. It is this use of exclusive-or
as opposed to the multiply and modulus that gives R250 a speed advantage over
a linear congruential method.
are
now words and the + is exclusive-or. It is this use of exclusive-or
as opposed to the multiply and modulus that gives R250 a speed advantage over
a linear congruential method.


Next: Quasi-Random Numbers
Up: Random WalksMarkov Chains
Previous: Linear Congruential Generators
Skip Carter
Tue Jan 9 12:38:54 PST 1996
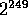 . What is more, this
period does not depend upon the number of bits used in the random
number generator. This makes 16-bit random numbers generated by R250,
adequate for many applications. The very long period makes it suitable for
scientific applications,
such as Monte Carlo and stochastic integration,
where many numbers need to be generated.
. What is more, this
period does not depend upon the number of bits used in the random
number generator. This makes 16-bit random numbers generated by R250,
adequate for many applications. The very long period makes it suitable for
scientific applications,
such as Monte Carlo and stochastic integration,
where many numbers need to be generated.
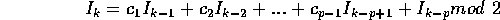
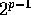 ,
so a large value of p is called for, we will use p = 250.
We now judiciously choose most of the
,
so a large value of p is called for, we will use p = 250.
We now judiciously choose most of the 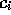 terms to be zero, so that there are
only two terms on the right hand side,
terms to be zero, so that there are
only two terms on the right hand side,

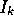 are
now words and the + is exclusive-or. It is this use of exclusive-or
as opposed to the multiply and modulus that gives R250 a speed advantage over
a linear congruential method.
are
now words and the + is exclusive-or. It is this use of exclusive-or
as opposed to the multiply and modulus that gives R250 a speed advantage over
a linear congruential method.