


Next: About this document ...
Up: number10
Previous: A nonlinear example
Now we understand what least squares estimation
is and are comfortable with how to use it to determine an optimal
estimate of the parameters system.
You probably won't be surprized to learn that this point that there
are other complicating factors that could be considered, but that
I have left them out for this introduction. You will notice that
we have assumed that when we make a measurement, that our knowledge
of 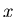 was exact and all the uncertainty/error was in
was exact and all the uncertainty/error was in 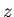 .
We can reformulate the equations to handle the situation where the
error is in
.
We can reformulate the equations to handle the situation where the
error is in 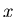 and not in
and not in 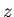 , or even when there are uncertainties
in both
, or even when there are uncertainties
in both 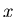 and
and 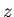 . We can also readily extend the
equations to handle the possibility that some
. We can also readily extend the
equations to handle the possibility that some 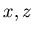 data measurements
are more accurate than others. I have also not shown you how to
write any of this in matrix form. While the linear algebra
formulation is extremely powerful, I have discovered after years of
being a professor that the mere mention of the term ``linear algebra''
causes students to quake in fear. Its really not that difficult a
subject, but I now know better than to spring in on anyone without
some prior preparation beforehand.
data measurements
are more accurate than others. I have also not shown you how to
write any of this in matrix form. While the linear algebra
formulation is extremely powerful, I have discovered after years of
being a professor that the mere mention of the term ``linear algebra''
causes students to quake in fear. Its really not that difficult a
subject, but I now know better than to spring in on anyone without
some prior preparation beforehand.
Least squares is the analytic tool that
we need to create an adaptive PID controller. Our model will be
the PID equations and the parameters are the gains. What we will
do next time is to work out the optimal estimators for a PID
controller and discuss how the estimation equations can be written
in a form suitable for a real-time system.
Please don't hesitate to
contact me through Forth Dimensions or
via e-mail at skip@taygeta.com if you have any comments
or suggestion about this or any other ForthWare column.
Skip Carter is a scientific and software consultant.
He is the
leader of the Forth Scientific Library project, and maintains the
system taygeta on the Internet. He is also the President of the
Forth Interest Group.



Next: About this document ...
Up: number10
Previous: A nonlinear example
Skip Carter
2008-08-20