


Next: A nonlinear example
Up: number10
Previous: Optimal estimation
The simplest example of the application of least
squares estimation is the fitting of data to a straight line.
In this problem, our model of the system is the equation for
a straight line,
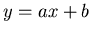 |
|
|
(1) |
where 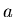 and
and 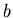 are the unknown adjustable parameters. If we
let
are the unknown adjustable parameters. If we
let 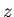 represent the measurements of what should be
represent the measurements of what should be 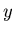 , i.e.,
, i.e.,
then we can define our cost function as:
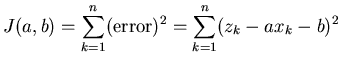 |
|
|
(2) |
To apply the least squares formalism to this, we need to figure out
how to minimize 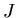 with respect to
with respect to 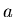 and
and 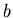 . We do this by
applying a little bit of calculus. The extreme values of a function
(maximum and minimum) occur where the derivative is zero.
The fact that it is straightforward to handle the derivative of a
squared quantity is what makes using the square more attractive than
the use of the absolute value.
We have two parameters, so we need to calculate the derivatives with
respect to both of them,
. We do this by
applying a little bit of calculus. The extreme values of a function
(maximum and minimum) occur where the derivative is zero.
The fact that it is straightforward to handle the derivative of a
squared quantity is what makes using the square more attractive than
the use of the absolute value.
We have two parameters, so we need to calculate the derivatives with
respect to both of them,
We need to expand these out and solve for 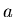 and
and 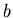 when both of
these equations are simultaneously set to zero.
when both of
these equations are simultaneously set to zero.
Now we have derived from (3),
![$\displaystyle 0 = -2 \left[ \sum_{k=1}^n x_k z_k - (a + b )\sum_{k=1}^n x_k^2 \right]$](img14.png) |
|
|
(5) |
and from (4),
![$\displaystyle 0 = -2 \left[ \sum_{k=1}^n z_k - a \sum_{k=1}^n x_k - b n \right]$](img15.png) |
|
|
(6) |
These can now be used to give equations for 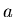 and
and 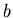 ,
,
for,
This is our optimal, least-squares, estimate of 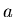 and
and 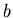 .
Note we should verify that this solution
is the minimum solution and not the maximum (remember
that the first derivative is zero at both places). This
verification requires taking the second derivatives and
establishing that they are positive.
This is pretty easy to show if one looks at (5) and (6). The
second derivative of
.
Note we should verify that this solution
is the minimum solution and not the maximum (remember
that the first derivative is zero at both places). This
verification requires taking the second derivatives and
establishing that they are positive.
This is pretty easy to show if one looks at (5) and (6). The
second derivative of 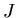 with respect to
with respect to 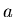 is the derivative
with respect to
is the derivative
with respect to 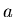 of the right hand side of (5), which is
of the right hand side of (5), which is
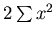 .
Since this is the sum of squared quantities it is positive so the
second derivative is positive. Doing the same for
.
Since this is the sum of squared quantities it is positive so the
second derivative is positive. Doing the same for 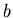 , we take
the derivative with respect to
, we take
the derivative with respect to 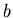 of the right hand side of
(6) and we get
of the right hand side of
(6) and we get 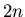 , which again is positive.
, which again is positive.
Listing 1, shows an example of a general purpose least squares
fit routine. It takes data pairs 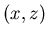 and returns the optimal
estimates of
and returns the optimal
estimates of 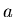 and
and 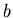 . For the sample data file in listing 2,
you should get a slope of 0.1781 and an intercept of 0.3687.
With a sufficient amount of patience (or by putting Mathematica
to work), we can work out equations like (7) and (8) for any
polynomial form, not just a straight line.
. For the sample data file in listing 2,
you should get a slope of 0.1781 and an intercept of 0.3687.
With a sufficient amount of patience (or by putting Mathematica
to work), we can work out equations like (7) and (8) for any
polynomial form, not just a straight line.



Next: A nonlinear example
Up: number10
Previous: Optimal estimation
Skip Carter
2008-08-20
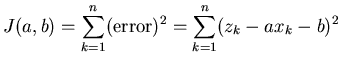
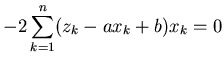
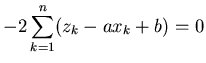
![]() and
and ![]() when both of
these equations are simultaneously set to zero.
when both of
these equations are simultaneously set to zero.
![$\displaystyle 0 = -2 \left[ \sum_{k=1}^n x_k z_k - (a + b )\sum_{k=1}^n x_k^2 \right]$](img14.png)
![$\displaystyle 0 = -2 \left[ \sum_{k=1}^n z_k - a \sum_{k=1}^n x_k - b n \right]$](img15.png)
![]() and
and ![]() ,
,
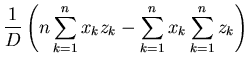
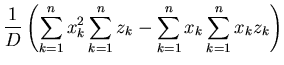
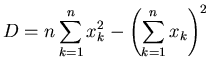
![]() and
and ![]() .
Note we should verify that this solution
is the minimum solution and not the maximum (remember
that the first derivative is zero at both places). This
verification requires taking the second derivatives and
establishing that they are positive.
This is pretty easy to show if one looks at (5) and (6). The
second derivative of
.
Note we should verify that this solution
is the minimum solution and not the maximum (remember
that the first derivative is zero at both places). This
verification requires taking the second derivatives and
establishing that they are positive.
This is pretty easy to show if one looks at (5) and (6). The
second derivative of ![]() with respect to
with respect to ![]() is the derivative
with respect to
is the derivative
with respect to ![]() of the right hand side of (5), which is
of the right hand side of (5), which is
![]() .
Since this is the sum of squared quantities it is positive so the
second derivative is positive. Doing the same for
.
Since this is the sum of squared quantities it is positive so the
second derivative is positive. Doing the same for ![]() , we take
the derivative with respect to
, we take
the derivative with respect to ![]() of the right hand side of
(6) and we get
of the right hand side of
(6) and we get ![]() , which again is positive.
, which again is positive.
![]() and returns the optimal
estimates of
and returns the optimal
estimates of ![]() and
and ![]() . For the sample data file in listing 2,
you should get a slope of 0.1781 and an intercept of 0.3687.
With a sufficient amount of patience (or by putting Mathematica
to work), we can work out equations like (7) and (8) for any
polynomial form, not just a straight line.
. For the sample data file in listing 2,
you should get a slope of 0.1781 and an intercept of 0.3687.
With a sufficient amount of patience (or by putting Mathematica
to work), we can work out equations like (7) and (8) for any
polynomial form, not just a straight line.