Consider the (vector) ordinary differential equation:
Now we suppose that the system has a random component,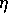 
, added to it,
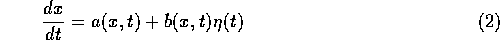
The solution to this random differential equation is problematic because the presence of randomness prevents the system from having bounded measure. The result is that the derivative does not exist.
One way to deal with equations such as (2), is to look at them in differential form,
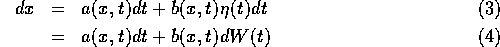
The solution to (2) or equivalently (3) or (4) can be regarded as the result of performing the integration,
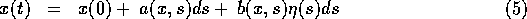
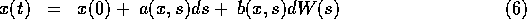
This definition of the solution to the stochastic differential equation (4) is consistent if we use the following for the chain rule:
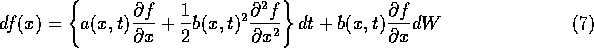
This equation is known as (the one dimensional) Itô's formula. This can be written in higher dimension as well.
The stochastic calculus we have just described is Itô calculus.
It is possible to define a consistent calculus and preserve the standard chain rule,
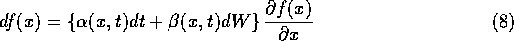
The integration
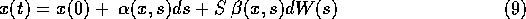
will be a solution to the SDE,
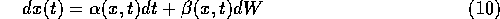
only if we define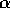 
and 
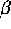in terms of our original equation (2)
as,
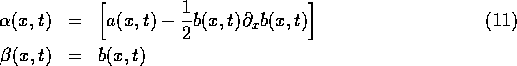
The resulting calculus is the Stratonovich calculus.
Everett F. Carter
Taygeta Scientific Inc.