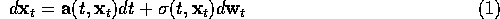
Consider the problem of numerically integrating the Itô stochastic differential equation,
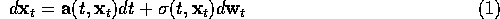
where 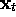 is a vector of dimension n,
is a vector of dimension n,  is a
vector function of dimension n,
is a
vector function of dimension n, 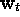 is a k-dimensional
Wiener process and
is a k-dimensional
Wiener process and 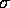 is an
is an 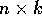 matrix valued function.
matrix valued function.
Milshtein (1978) derived the following scheme for numerically solving (1),
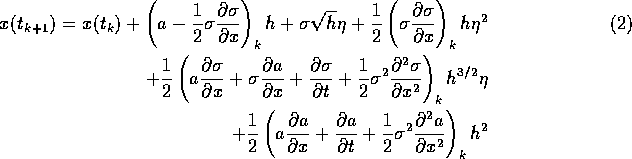
(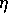 is a Gaussian random variable with zero mean and unit variance).
is a Gaussian random variable with zero mean and unit variance).
This scheme is 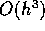 , and
, and 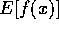 is
is 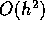 .
.
The above scheme is not used in the implementation of software to do the calculation because of the difficuties the high derivatives that need to be evaluated at each step. Therefore for numerical use, the following scheme is used,
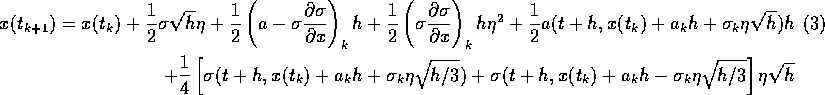
Milshtein, shows that (3) is equivalent to (2).