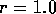 )
is held at a constant 40 degrees, and the outer radius
(
)
is held at a constant 40 degrees, and the outer radius
(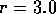 ) is held at 60
degrees. The equation describing this situation is:
) is held at 60
degrees. The equation describing this situation is:
One of the classic scientific applications of the Monte Carlo method is in the solution of differential equations. The cautions about the applicability of Monte Carlo that were mentioned earlier, are especially important here.
Using Monte Carlo to solve differential equations is very inefficient, but if there are special conditions then it might be the best way to go. The idea here is to set up a random walk within the domain that the equation applies, starting at the point at which we want the solution. The probability of moving in each possible direction is determined by the differential equation that is being solved, it is not necessarily the same in each direction. The random walk continues until the particle reaches the boundary of the domain. At this point the particle may be absorbed, the probability of this occuring depends upon the type of boundary condition that applies at that point. If the particle is not absorbed, the walk continues on until it reaches a boundary and finally does get absorbed.
As a simple example, let us consider the steady state temperature
distribution of a annulus. Lets assume that the inner radius (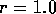 )
is held at a constant 40 degrees, and the outer radius
(
)
is held at a constant 40 degrees, and the outer radius
(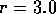 ) is held at 60
degrees. The equation describing this situation is:
) is held at 60
degrees. The equation describing this situation is:

The standard finite difference approximation to this (assume the same size grid, h, in both x and y) is,
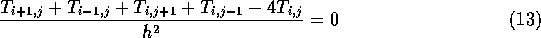
This can be rearranged to,
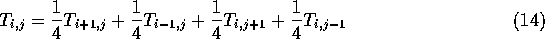
Now we interpret equation (14) to mean that if at some time we are at position
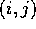 , then at the next step we go to one of each of the four surrounding points
with probability 1/4. This is the standard random walk.
, then at the next step we go to one of each of the four surrounding points
with probability 1/4. This is the standard random walk.
So to solve the problem, we start out at the position we would like to have the solution at, and do our random walk until we reach a boundary, (because the mean squared distance from a starting point is linearly proportional to time, we will eventually reach a boundary). For our example problem the temperature is given on two boundaries, so when we reach a boundary we keep that value. We do many such walks, and our estimate will be the mean of the boundary values that we encountered.