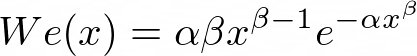
This is a step-by-step explaination of how to calculate a transformation function that converts a random variable of one distribution to another distribution. This example uses the Weibull distribution as the intended target distribution.
The Weibull distribution is defined as follows,
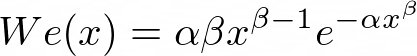
The parameters alpha and beta are greater than zero. For values of x less than zero, the distribution is defined to be zero.
The mean for this distribution is:
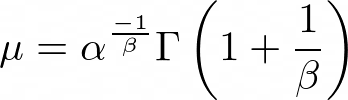
The variance is:
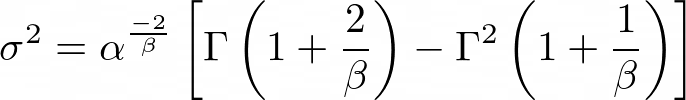
To determine the transformation we start with the fundamental transformation law of probabilities for two probability distribution functions f(y) and p(x),
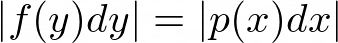
or,
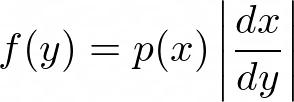
This allows us to relate a random variable x from the distribution function p(x) with the random variable y from the distribution function f(y). If x is from a uniform distribution in [0,1], then p(x) is constant so we have,
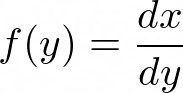
The solution to this is the definite integral of f(y),
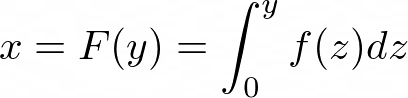
This relationship gives us the source random variable, given the target random variable. So we need to be able to invert the relationship,
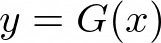
It is the difficulty of the determination of y = G(x) given x = F(y) that makes this problem potentially infeasible.
For the case of the Weibull distribution we can readily determine the inverse.
Starting with,
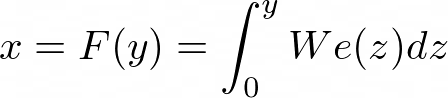
then doing this integral we get,
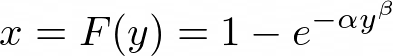
Now we need to invert this to write, y = G(x),
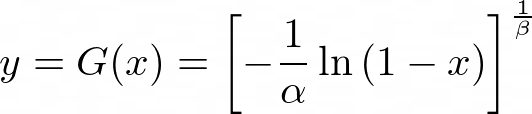
Finally, the transformation is:
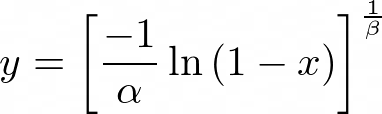
We start with the random number, x, which comes from a uniform distribution (in the range from 0 to 1). Then apply the above transformation to get a new independent random number which has a Weibull distribution with a mean and variance that depends upon the values of alpha and beta.
function [WeibullRandomNumbers]=WeibullRNG(scale,shape,noOfRandomNumbers) %Written by David Vannucci 01 June 2003 devannucci@yahoo.com WeibullRandomNumbers = scale.*( -log(1-rand(noOfRandomNumbers,1))).^(1/shape);
Knuth, D.E., 1981; The Art of Computer Programming, Volume 2 Seminumerical Algorithms, Addison-Wesley, Reading Mass., 688 pages, ISBN 0-201-03822-6
Press, W.H., B.P. Flannery, S.A. Teukolsky, W.T. Vetterling, 1986; Numerical Recipes, The Art of Scientific Computing, Cambridge University Press, Cambridge, 818 pages, ISBN 0-512-30811-9
|
|