Random Number Generation,
Why Should I care ?
Here is a case where a poor random number generator can have a
big impact on your conclusions of your scientific research.
The following figures show the result of using the
3rd Order Milshtein method for SDEs to integrate the following
system of Ito Stochastic differential equations:
dx = - f0 sin( f0 t ) dt + sqrt( q0 ) dw1
dy = - f1 sin( f1 t + delta ) dt + sqrt( q1 ) dw2
The values of f0, f1, delta, q0 and q1 are constants.
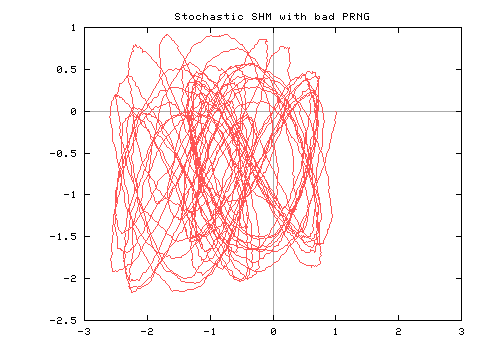
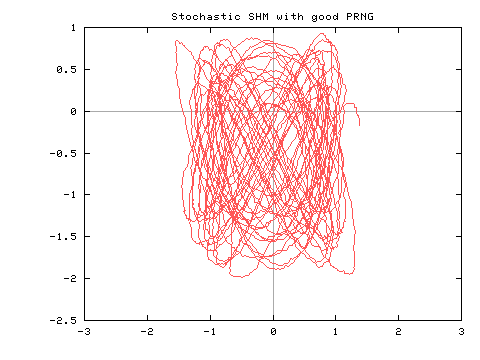
Note that in both cases the same parameter values and initial condition was used.
If you were to study the first case you might conclude that you were looking
at a nonstationary system (slowly drifting off to the lower left),
but that's just an artifact of the PRNG!
The bottom line is, if you do any serious stochastic modelling, review
the literature on PRNGs and choose the appropriate one to implement and
use.
Back to Taygeta's Random Number page.
Taygeta's home page