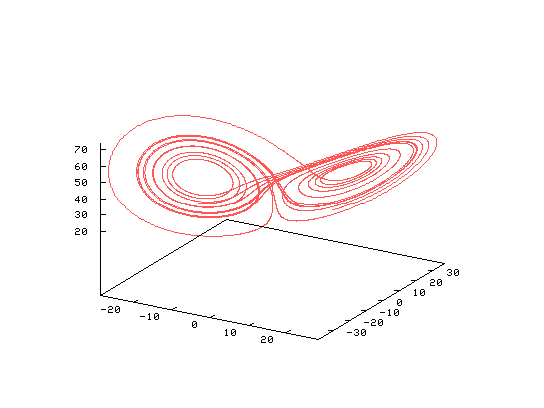

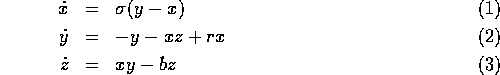
The parameter r is the ratio of the Rayleigh number divided by the
critical Rayleigh number. The parameter 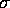 is the Prandtl number.
The third parameter b is related to the horizontal wave number of the system.
Typical values, r = 28,
is the Prandtl number.
The third parameter b is related to the horizontal wave number of the system.
Typical values, r = 28, 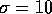 ,
, 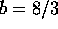 , dimension
, dimension 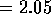 . A common
second set of values,
. A common
second set of values, 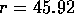 ,
, 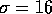 , b = 4, dimension
, b = 4, dimension 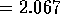 .
.
The interesting cases are where the Rayleigh number ratio, r, is large which suggests that we could expand the system of equations around a parameter which is proportional to the reciprocal of r (which would be small).
If we define,

and let,
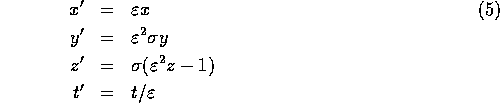
Then equations (1) - (3) become (after dropping the primes),
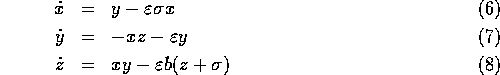
Now consider the expansion of x, y, and z in terms of the parameter
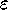 ,
,
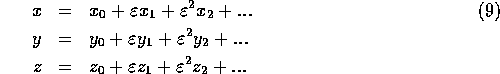
Introducing (9) in (6) - (8), gives the order 0 equations,

and at order 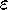 , the system,
, the system,
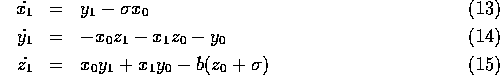
The interdependence of the first order equations with the order 0 equations can removed with some algebraic manipulation,
Use (11) and (12) to eliminate 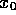 ,
,

Integrating this,
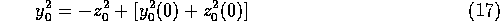
where the terms in the brackets of equation (17) are the initial values of
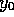 and
and 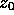 .
We will define this (constant) term as
.
We will define this (constant) term as

If we go back to (10) and (12) to eliminate 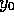 ,
,

Integrating this gives,
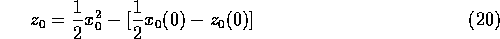
here the terms in the brackets of equation (20) are the initial values of
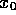 and
and 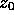 .
.
We will define this term as,

Using (17) in (10) gives,

now using (19),
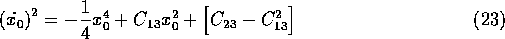
Given the solution to this equation, 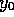 can be solved for by using (10).
Then given
can be solved for by using (10).
Then given 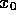 and
and 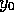 , then
, then 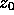 can be solved for by using (12).
An equation for
can be solved for by using (12).
An equation for 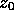 can also be derived by using
manipulations similar to that used in deriving (23)
(using equations (17) and (20) in (12) to eliminate
can also be derived by using
manipulations similar to that used in deriving (23)
(using equations (17) and (20) in (12) to eliminate
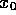 and
and 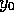 ), to give,
), to give,
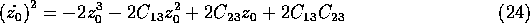
Equation (23) can be solved analytically, its solution is a Jacobi elliptic function,

The other components can also be determined,
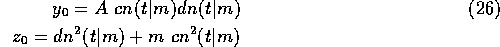
(where 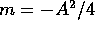 )
so the system is well behaved (not chaotic).
)
so the system is well behaved (not chaotic).
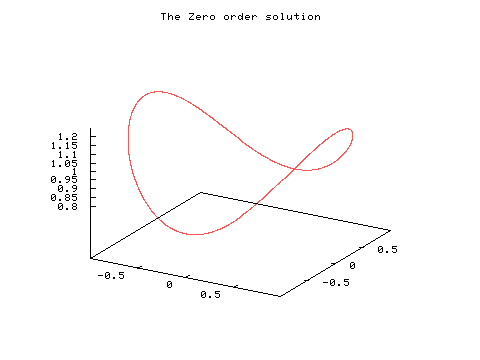
The first order equations ( (13) - (15) ) are linear so they cannot possibly lead to chaotic solutions (all subsequent order equations are also linear). Thus we have shown that while the actual system can be chaotic, the perturbation solutions may not be.
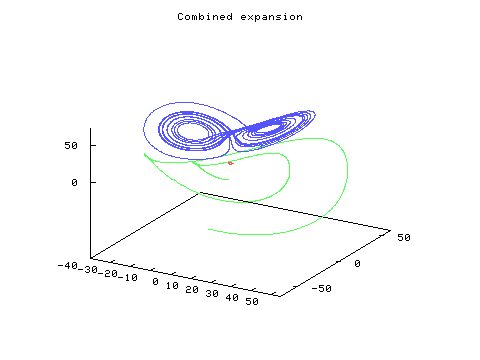
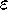 times the solution of
(13) - (15) added to the zero order solution, in green). The perturbation solution
tracks the nonlinear solution for a short while then it moves off in a
different direction. The perturbation solution also rapidly grows to order
one, so that the expansion (9) is valid for only a limited time.
times the solution of
(13) - (15) added to the zero order solution, in green). The perturbation solution
tracks the nonlinear solution for a short while then it moves off in a
different direction. The perturbation solution also rapidly grows to order
one, so that the expansion (9) is valid for only a limited time.