


Next: Convolutions and Digital Filters
Up: number8
Previous: Introduction
We will start by defining a transform function that
at first looks so trivial that it appears that it cannot possibly
be useful. Let us assume that data is digitized at a uniform
sampling rate. Say our data consisted of the sequence of points:
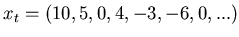 |
|
|
(1) |
We can represent this data as a polynomial:
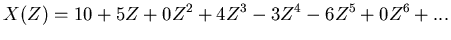 |
|
|
(2) |
This polynomial is called the Z transform of the time series.
The trick with Z transforms is how we interpret what the 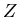 actually
represents. The
actually
represents. The 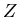 is called the unit delay operator because
of the following, if we take (2) and multiply it by
is called the unit delay operator because
of the following, if we take (2) and multiply it by 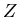 we get,
we get,
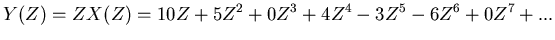 |
|
|
(3) |
which becomes the untransformed series:
which is just the original time series delayed by one unit of time
(Be careful if you try to look the Z transform up in a book. In a
variation of the pi throwing contest that I mentioned a few columns
back, different authors use different sign conventions on the Z
transform polynomial.).
This innocent looking transform and delay operator turn out to be
very powerful. Consider the following, suppose that 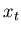 represents
the response of the ground to an explosion (which we will call the
impulse response). If another explosion occurred 10 time units
later, then the signal that we would see is
represents
the response of the ground to an explosion (which we will call the
impulse response). If another explosion occurred 10 time units
later, then the signal that we would see is
which can be represented by
If the second explosion was half the strength of the first, then
we'd write,
If the second was a half strength implosion, then the sign
is just reversed,
If the second signal came in overlapping the first (say at time 4)
then the numbers in the series is a bit messy looking,
but rest assured this series can be written out as having the
transform,
A Forth function to do this kind of factorization is shown in
listing 1. This code has been contributed to the
Forth Scientific Library and is awaiting review for its acceptance.
(Volunteers for doing code reviews are eagerly accepted!).
In general we can do this for an arbitrarily complicated sequence
of explosions and implosions as long as the response of the
earth remains linear (an example of a nonlinear response
would be the state of the ground within a mile or so of a nuclear
explosion).
So suppose we have a sequence consisting of an explosion at 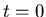 , a
half strength implosion at time
, a
half strength implosion at time 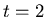 and a quarter strength
explosion at time
and a quarter strength
explosion at time 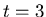 ,
,
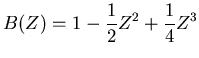 |
|
|
(6) |
then,
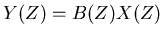 |
|
|
(7) |
Now without doing any integrals, and just manipulating polynomials
we have done the convolution theorem,
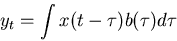 |
(8) |
Both equations (7) and (8) state that
the signal 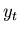 is the convolution of
is the convolution of 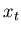 and
and 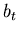 , but the
Z transform version just involves simple manipulation of polynomials.
Listing 2 provides an implementation of convolution algorithms, this
code is also an unreviewed contribution to the Forth Scientific
Library.
, but the
Z transform version just involves simple manipulation of polynomials.
Listing 2 provides an implementation of convolution algorithms, this
code is also an unreviewed contribution to the Forth Scientific
Library.



Next: Convolutions and Digital Filters
Up: number8
Previous: Introduction
Skip Carter
2008-08-20
![]() represents
the response of the ground to an explosion (which we will call the
impulse response). If another explosion occurred 10 time units
later, then the signal that we would see is
represents
the response of the ground to an explosion (which we will call the
impulse response). If another explosion occurred 10 time units
later, then the signal that we would see is
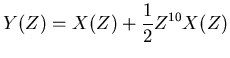
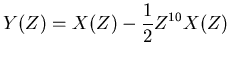
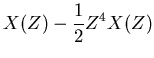
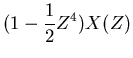
![]() , a
half strength implosion at time
, a
half strength implosion at time ![]() and a quarter strength
explosion at time
and a quarter strength
explosion at time ![]() ,
,
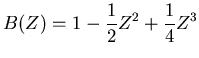
![]() is the convolution of
is the convolution of ![]() and
and ![]() , but the
Z transform version just involves simple manipulation of polynomials.
Listing 2 provides an implementation of convolution algorithms, this
code is also an unreviewed contribution to the Forth Scientific
Library.
, but the
Z transform version just involves simple manipulation of polynomials.
Listing 2 provides an implementation of convolution algorithms, this
code is also an unreviewed contribution to the Forth Scientific
Library.