


Next: Fine tuning a PID
Up: number7
Previous: Improving the Controller
We can use all three terms together and get the
proportional-integral-derivative controller.
The equation that fully describes the PID control is:
where 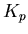 is the proportional gain,
is the proportional gain, 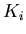 is the integral gain
and
is the integral gain
and 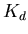 is the differential gain.
For a practical implementation on a digital system, the above
equation is replaced with a discrete time approximation:
is the differential gain.
For a practical implementation on a digital system, the above
equation is replaced with a discrete time approximation:
where we have used a rectangle approximation to the integral and
a backward difference approximation for the derivative.
These are rather crude numerical approximations but we will generally
be able to compensate for this by making the discrete sampling rate
fast and by tuning the controller. The
simple numerics has the great virtue of being very easy to implement.
Skip Carter
2008-08-20
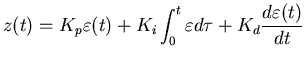
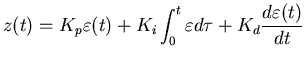
![$\displaystyle z(k) = K_p \varepsilon(k) + K_i \sum_{j=0}^{k} \varepsilon(j)
+ K_d \left[ \varepsilon(k) - \varepsilon(k-1) \right]$](img10.png)