


Next: The controller equations
Up: number11
Previous: Introduction
While there is a good deal of mathematics behind
adaptive controllers, its not particularly hard mathematics.
The reason for this is that traditionally most controllers are
linear. We can take advantage of this linearity to make
the equations relatively easy to manipulate. Lets first consider
what is means for a system to be linear. Essentially, linearity
means that the system obeys a superposition principle. Suppose
that 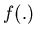 represents our system and further that
represents our system and further that 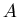 and
and 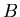 are two valid but otherwise arbitrary solutions to
are two valid but otherwise arbitrary solutions to 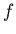 .
Then if it is true that,
.
Then if it is true that,
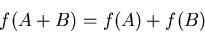 |
(1) |
then the system is said to be linear.
Many familiar systems have this property.
It is equation (1) that allows us to decompose a
periodic signal into frequency bands and calculate a power spectrum.
Potential fields (electric, magnetic and gravitational) are also
linear. The main reason why linear systems are so familiar, is
not because they are so ubiquitous (in fact, one author
has pointed out that dividing nature into linear and nonlinear
systems is like having ``nonelephant'' biology as a special subfield,
and missing the fact that most systems are not linear), but because
equation (1) makes linear systems solvable. Many nonlinear systems
are handled by making them approximately linear, e.g.:
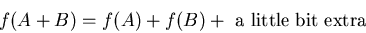 |
(2) |
The work then primarily concentrates on how small that little bit
actually is and under what circumstances is stays small. For
many nonlinear systems (2) is a practical approach that gives
useful answers. Systems that can be analyzed this way generally
get described with phrases like ``small amplitude''; a dead giveaway
that something like (2) was used. A simple example of this is the
ordinary pendulum. A pendulum is actually a nonlinear system, but
for small amplitude excursions (say 10 degrees), the nonlinear
effects are extremely small and can be ignored for typical
applications. Some nonlinear systems cannot be broken down
to something like (2) without completely missing the real solutions.
Any system that has chaotic behavior is like this, the chaos comes
from the nonlinearity; there are no chaotic systems that are linear.
Many methods have been invented for dealing with linear systems,
one that we will find useful here is the Laplace transform.
For the system 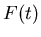 the Laplace transform
the Laplace transform
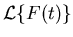 is defined
by,
is defined
by,
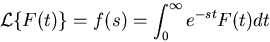 |
(3) |
(strictly speaking this applies only for 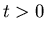 ).
There are two properties that make the Laplace transform particularly
suited to our problem:
).
There are two properties that make the Laplace transform particularly
suited to our problem:
- Like the Fourier transform, it converts a linear differential
equation into a polynomial. (you might not have realized this, but
we can transform - Fourier or Laplace - an equation, not
just a stream of data).
- Unlike the Fourier transform, it treats transients efficiently.
The Laplace transform is, in fact, the impulse response function
for a system.
Its a bit tedious to do the integrations required to do either
a forward or inverse transform by hand, so the Laplace
transform is often done with the help of symbolic integration
software or the use of tables in a handbook. Table 1 gives the
Laplace tranform for several useful mathematical functions.
Combining this with some general transformation properties given
in Table 2, gives us the ability to determine the Laplace tranform
of a large number of useful functions without the need to explicitly
solve (3).
The forward Laplace
transform is not too difficult to do numerically, but calculating
the inverse transform numerically leads to problems with the
numerical stability of the calculation; this is not a problem with
software that is capable of doing the inverse tranform symbolically.
We will use the Laplace tranform to work out how the controller will
respond to its inputs. We need to do be able to do this because there
is no unique way to set up an adaptive controller - a motor speed
controller that uses a shaft angle encoder will be quite different
from one that uses a tachometer.



Next: The controller equations
Up: number11
Previous: Introduction
Skip Carter
2008-08-20
![]() the Laplace transform
the Laplace transform
![]() is defined
by,
is defined
by,